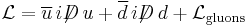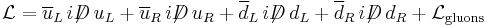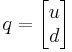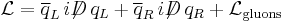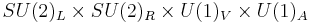Chiral symmetry

In quantum field theory, chiral symmetry is a possible symmetry of the Lagrangian under which the left-handed and right-handed parts of Dirac fields transform independently. The chiral symmetry transformation can be divided into a component that treats the left-handed and the right-handed parts equally, known as vector symmetry, and a component that actually treats them differently, known as axial symmetry.

Example: u and d quarks in QCD

Consider quantum chromodynamics (QCD) with two massless quarks u and d. The Lagrangian is

$\mathcal{L} = \overline{u}\,i\displaystyle{\not}D \,u %2B \overline{d}\,i\displaystyle{\not}D\, d %2B \mathcal{L}_\mathrm{gluons}$

In terms of left-handed and right-handed spinors it becomes

$\mathcal{L} = \overline{u}_L\,i\displaystyle{\not}D \,u_L %2B \overline{u}_R\,i\displaystyle{\not}D \,u_R %2B \overline{d}_L\,i\displaystyle{\not}D \,d_L %2B \overline{d}_R\,i\displaystyle{\not}D \,d_R %2B \mathcal{L}_\mathrm{gluons}$

(Hereby i is the imaginary unit and 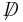$\displaystyle{\not}D$ the well-known Dirac operator.)

Defining

$q = \begin{bmatrix} u \\ d \end{bmatrix}$

it can be written as

$\mathcal{L} = \overline{q}_L\,i\displaystyle{\not}D \,q_L %2B \overline{q}_R\,i\displaystyle{\not}D\, q_R %2B \mathcal{L}_\mathrm{gluons}$

The Lagrangian is unchanged under a rotation of 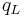$q_L$ by any 2 x 2 unitary matrix L, and 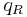$q_R$ by any 2 x 2 unitary matrix R. This symmetry of the Lagrangian is called flavor symmetry or chiral symmetry, and denoted as 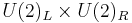$U(2)_L \times U(2)_R$ . It can be decomposed into

$SU(2)_L \times SU(2)_R \times U(1)_V \times U(1)_A$

The vector symmetry 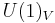$U(1)_V\,$ acts as

$q_L \rightarrow e^{i\theta} q_L \qquad q_R \rightarrow e^{i\theta} q_R$

and corresponds to baryon number conservation.

The axial symmetry 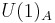$U(1)_A\,$ acts as

$q_L \rightarrow e^{i\theta} q_L \qquad q_R \rightarrow e^{-i\theta} q_R$

and it does not correspond to a conserved quantity because it is violated due to quantum anomaly.

The remaining chiral symmetry 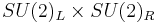$SU(2)_L \times SU(2)_R$ turns out to be spontaneously broken by quark condensate into the vector subgroup 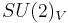$SU(2)_V\,$ , known as isospin. The Goldstone bosons corresponding to the three broken generators are the pions. In real world, because of the differing masses of the quarks, 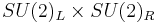$SU(2)_L \times SU(2)_R$ is only an approximate symmetry to begin with, and therefore the pions are not massless, but have small masses: they are pseudo-Goldstone bosons.^[1]

References

^ Peskin, Michael; Schroeder, Daniel (1995). An Introduction to Quantum Field Theory. Westview Press. pp. 670. ISBN 0201503972.